PRISMA

Prisma proviene del latín prisma y tiene su antecedente más remoto en un vocablo griego. En el ámbito de la geometría, se conoce como prisma a un cuerpo cuyos límites lo establecen un par de polígonos iguales y planos, dispuestos de forma paralela, y diversos paralelogramos, de acuerdo a la cantidad de lados que dispongan sus bases. Esto quiere decir que si las bases son triángulos, estaremos hablando de un prisma triangular.

ELEMENTOS DE UN PRISMA

Elementos de un prisma:

Cada prisma consta de los siguientes elementos:

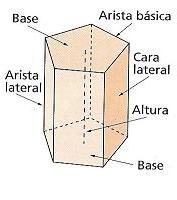
· Bases: son las dos caras iguales y paralelas del prisma, una en la que se apoya y la otra su opuesta.

· Caras laterales: son las caras que comparten dos de sus lados con las bases. La suma de sus áreas es la superficie lateral del prisma.

· Aristas: son los lados de las bases y de las caras laterales.


· Vértices: son los puntos en donde se encuentran cada par de aristas.

· Altura: es la distancia entre las bases.

· Diagonales: son los segmentos que unen dos vértices no consecutivos del prisma. Se pueden trazar las diagonales de una cara o entre dos caras.

CLASIFICACIÓN DE LOS PRISMAS

Los prismas se clasifican según la forma de sus caras laterales en:

Prismas rectos: Son aquellos cuyas caras laterales son rectángulos o cuadrados. Sus aristas laterales son perpendiculares a las bases.
Prismas oblicuos: Son aquellos cuyas caras laterales son paralelogramos que no son rectángulos ni cuadrados. Sus aristas laterales no son perpendiculares a las bases.

A su vez, los prismas rectos se clasifican en:

Prismas regulares: Son aquellos cuyas bases son polígonos regulares.
Prismas irregulares: Son aquellos cuyas bases son polígonos irregulares.

AREA DEL PRISMA

Como vemos, este prisma hexagonal tiene 6 caras laterales que son rectángulos y 2 bases que son hexágonos.

El área lateral de un prisma es la suma de las áreas de sus caras laterales (los 6 rectángulos).

Las 6 caras laterales forman un rectángulo cuya base es el perímetro del hexágono de la base. 

Por tanto, el área lateral del prisma es igual al producto del perímetro de la base por la altura:

Área lateral = perímetro de la base x altura

El área total es la suma del área lateral más el área de las 2 bases:

Área total = Área lateral + Área de la base x 2

VOLUMEN DEL PRISMA

El volumen del prisma recto se calcula multiplicando las longitudes de las tres aristas convergentes a un vértice. Por ejemplo, si las aristas de un prisma recto son 2, 3 y 6 cm entonces el volumen del mismo se obtiene multiplicando 2 x 3 x 6:

V = 2cm x 3cm x 6cm = 36cm³

Por lo tanto, si las tres aristas concurrentes a un vértice miden a, b y c entonces su volumen se calcula a través de la fórmula:

V = a.b.c

El volumen de un prisma se puede también definir como el producto del área de la base por la altura, es decir:

V = Área base x altura

En el ejemplo: V = (3cm x 2 cm) x 6 cm = 6cm² x 6cm = 36cm³

Si el prisma no es recto, su volumen, según el principio de Cavalieri, será el mismo que el del prisma recto con igual sección y altura. La única diferencia es que, en este caso, la altura no coincide con la arista lateral.

Por ejemplo, si las aristas de la base de un prisma oblicuo miden 3cm y 2cm, y su altura mide 4cm entonces su volumen se calcula a través de la fórmula del prisma recto:

V = Área de la base x altura

V = (3cm x 2cm) x 4cm = 6cm² x 4cm = 24cm³

Prismas y Piramides

En geometría, un prisma es un poliedro con una base poligonal de n lados, una copia de traslación (no en el mismo plano que la primera), y otras n caras (todas necesariamente deben ser paralelogramos) que une los lados correspondientes de las dos bases. Todas las secciones transversales paralelas a las caras de la base son iguales. Los prismas se nombran para su base, por lo que un prisma de base pentagonal se llama un prisma pentagonal. Los prismas son una subclase de los prismatoides.

https://www.youtube.com/watch?v=us1OLGStlAE